REM Subgroup 1: Modes and Surface Waves

Latest Updates

This page provides tables, diagrams and links for mode and surface wave data. Summarized are published and unpublished values for mean frequencies, mean attenuation for fundamental modes and overtones, for all types of motion: radial, spheroidal (Rayleigh Waves) and toroidal (Love Waves).

Subgroup coordinator: Guy Masters

ContributorsLinks
Durek
Ekström ftp://saf.harvard.edu/pub/PVmaps
Laske ftp://carp.ucsd.edu/pub/gabi/phase
Li
Masters ftp://carp.ucsd.edu/pub/guy/minos.dir
Montagner
Ritzwoller/Resovsky Colorado Normal Mode web site
Romanowicz
Trampert ftp://ftp.geo.uu.nl/pub/people/jeannot
Tromp Harvard Normal mode web site
Um
Widmer-Schnidrig Regionalized Multiplet Stripping
Zhang
If you would like to contribute, please contact Guy Masters
( gmasters@ucsd.edu)

Assembled Data Sets

Frequencies of free oscillations and surface waves

The linked diagrams compare published and unpublished values for mean frequencies for various types of motion (spheroidal/Rayleigh wave; toroidal/Love wave and radial) for fundamental modes and the first few overtone branches.

For the fundamental modes, most low harmonic degree values are from applications of iterative spectral fitting, with a few values coming from averages of singlet frequencies determined by singlet stripping. Higher l values are from surface wave analyses.

Contributors:
  • Preliminary Reference dataset: smodes/tmodes
  • Modes
    • RMG86: Ritzwoller, Masters and Gilbert (1986)
    • S&M: Smith and Masters (1989)
    • RR&M: Roult, Romanowicz and Montagner (1990)
    • WZ&M: Widmer, Zürn and Masters (1992)
    • SS: Masters (single stripping), unpublished
    • Tromp:
    • H&T: He and Tromp
    • Um:
    • Li:
    • R&R: Ritzwoller and Resovsky
    • M&W: Masters and Widmer
    • M&L: Masters and Laske (1998)
    • D&R: Durek and Romanowicz
  • Surface Waves
    • Wong: Wong (1989)
    • Mont: Montagner and Tanimoto (1990)
    • L&M: Laske and Masters (1996)
    • T&W: Trampert and Woodhouse (1996)
    • ET&L: Ekström, Tromp and Larson (1997)
The tables can be downloaded onto your machine by opening the table and saving it with the save option of your web program.

top
top of data
top of frequencies
bottom

Attenuation of free oscillations and surface waves

The linked diagrams compare published and unpublished values for q (1000/Q) for various types of motion (spheroidal/Rayleigh wave; toroidal/Love wave and radial) for fundamental modes and the first few overtone branches.

Most low harmonic degree values are from applications of iterative spectral fitting, with a few values coming from averages of singlet q's determined by singlet stripping. Higher l values are from surface wave analyses.

NB: The discrepancies between mode and surface wave analyses are discussed in several recent manuscripts -- references will be provided as they become available.

Contributors:
  • Preliminary Reference dataset: smodes/tmodes
  • Modes
    • Wid/Mast: Widmer and Masters
    • Li (1990)
    • Maste(ss): Masters (singlet stripping), unpublished
    • Um: Um (iterative spectral fitting), unpublished
    • Tromp: He and Tromp (1996)
    • Res/Ritz: Resovsky and Ritzwoller
  • Surface Waves
    • Durek: Durek and Ekström (1996)
    • Roman: Romanowicz, unpublished
    • Laske: Laske, unpublished

The tables can be downloaded onto your machine by opening the table and saving it with the save option of your web program.
top
top of data
top of attenuation
bottom

Free oscillation structure coefficients

NEW:A "best estimate" set of structure coefficients are now available up to degree and order 6. Go to the cst web page.

Comparison of Harmonic Degree 2

Harmonic degree 2 structure coefficients for fundamental modes made by modal analyses and surface wave analyses. Agreement between the various studies is quite good though the mode analysis of RR&M seems to give values which are inconsistent with other studies at harmonic degrees greater than 60. Surface wave studies which use only minor arc data do not seem to reliably constrain degree 2 but studies at low angular order but studies which use great circle data give answers which are generally consistent with the modal analyses. We conclude that a "reference dataset" for degree 2 structure coefficients up to moderate angular order can be determined.

Spheroidal fundamental modes high angular order
Toroidal fundamental modes high angular order
top
top of data
top of structure coefficients
bottom

Surface Wave Dispersion maps

These are examples of data sets that could constrain the 3D short-wavelength structure of the new 3D reference model. Such maps are composed at various frequencies and are then inverted for 3D mantle structure. There is general agreement about the location of long-wavelength structure. But the small-scale features still vary considerably from author to author.

Surface wave maps of various work groups are shown at two periods: 150s/6mHz and 50s/12mHz (frequencies are chosen to allow a qualitative comparison). Anomalies are percentage phase velocity perturbations. The signal in the shorter period maps is usually larger than in the longer period ones, indicating that 3D structure is concentrated at shallower depth. The maps are expanded in surface spherical harmonics where the truncation level is indicated in the table below.
Rayleigh wave maps
Love wave maps

Amplitude spectra

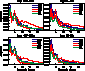The spectra are shown only up to harmonic degree l=24. They are normalized so that the spectrum of a delta-function would be flat.

While the long-wavelength patterns generally agree in phase, there is still some disagreement in the spectral amplitude. The maps with low amplitudes at harmonic degrees 1-5 are inconsistent with our (L&M) phase data. The ones with high amplitudes at high harmonic degree (rough maps) cannot explain our polarization data (which are particularly sensitive to short-wavelength structure).

Contributors

Referencelmaxobtain coefficients
ET&LEkström, Tromp and Larson (1997)36 web site anonymous ftp
L&MLaske and Masters (1996)24 web site anonymous ftp
T&WTrampert and Woodhouse (1996)40 email anonymous ftp
M&TMontagner and Tanimoto (1991)15 email
Z&LZhang and Lay (1996)24/28 email Thorne

G. Ekström, J. Tromp and E. Larson, Measurements and global models of surface wave propagation. J. Geophys. Res.,102, 8137-8157, 1997.

G. Laske and G. Masters, Constraints on global phase velocity maps from long-period polarization data. J. Geophys. Res.,101, 16,059-16,075, 1996.

J. Trampert and J.H. Woodhouse, High-resolution global phase velocity distributions. Geophys. Res. Let.,23, 21-24, 1996.

J.P. Montagner and T. Tanimoto, Global anisotropy in the upper mantle inferred from the regionalization of phase velocities. J. Geophys. Res.,96, 20,337-20,351, 1991.

Y.-S. Zhang and T. Lay, Global surface wave phase velocity variations. J. Geophys. Res.,101, 8415-8436, 1996.

top
top of data
top of phase velocity maps
Go back to List of subgroups
Go back to main page
Gabi Laske ( glaske@ucsd.edu)